sprechen
Member
I am restoring a 1923 Steirische 3 row in Bb/Eb/Ab. I have done some tuning on others but not on this box. Now i am confused (
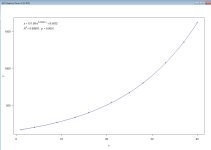
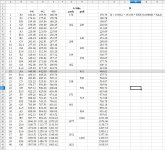
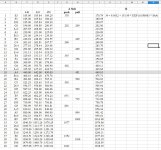
could be my age 79)! It's badly out of tune and this is what is confusing to me, I am using Strobe by Peterson and when I measure an A4 reed I get the following results. 1) Concert A set to 440, +16 cents, Hz 498.5 2) Concert A set to 445, -4 cents, Hz 498.5 3) Concert A set to 450, -23 cents, Hz 498.5.
Since the reed is always at 498.5 Hz,( irregardless of where the concert pitch is set) why doesn't the app say the reed is a B4 instead of an A4 when set to A=440?
Also, what is the best way to determine what pitch was the box originally tuned to? After looking at lots of measurements and trying to do some averaging I think its about 450.
Thanks for any help
could be my age 79)! It's badly out of tune and this is what is confusing to me, I am using Strobe by Peterson and when I measure an A4 reed I get the following results. 1) Concert A set to 440, +16 cents, Hz 498.5 2) Concert A set to 445, -4 cents, Hz 498.5 3) Concert A set to 450, -23 cents, Hz 498.5.
Since the reed is always at 498.5 Hz,( irregardless of where the concert pitch is set) why doesn't the app say the reed is a B4 instead of an A4 when set to A=440?
Also, what is the best way to determine what pitch was the box originally tuned to? After looking at lots of measurements and trying to do some averaging I think its about 450.
Thanks for any help